C++ 利用硬件加速矩阵乘法
本文共 2946 字,大约阅读时间需要 9 分钟。
文章目录
一、矩阵乘法定义
- 矩阵 A x × y A_{x \times y} Ax×y 和 矩阵 B u × v B_{u \times v} Bu×v 相乘的前提条件是 y = = u y==u y==u ,并且相乘后得到的矩阵为 C x × v C_{x \times v} Cx×v(即 A A A 的行和 B B B 的列构成了矩阵 C C C 的行列);
二、矩阵类封装
- 我们用 C++ 封装了一个 n × m n \times m n×m 的矩阵类,用二维数组来存储数据,定义如下:
#define MAXN 1000#define LL __int64class Matrix { private: int n, m; LL** pkData;public: Matrix() : n(0), m(0) { pkData = NULL; } void Alloc() { pkData = new LL *[MAXN]; // 1) for (int i = 0; i < MAXN; ++i) { pkData[i] = new LL[MAXN]; } } void Dealloc() { if (pkData) { for (int i = 0; i < MAXN; ++i) { // 2) delete [] pkData[i]; } delete[] pkData; pkData = NULL; } }}; - 1) p k D a t a pkData pkData 可以认为是一个二维数组( p k D a t a [ i ] [ j ] pkData[i][j] pkData[i][j] 就是矩阵第 i 行,第 j 列的数据),之所以这里用了二维指针,是因为当 MAXN 很大时,栈上分配不了这么多空间,容易导致栈溢出,所以通过 new 把空间分配在了堆上;
- 2)释放空间的时候,首先释放低维空间,再释放高维空间;
三、矩阵乘法实现
1、 i j k ijk ijk 式
- 最简单的矩阵乘法实现如下:
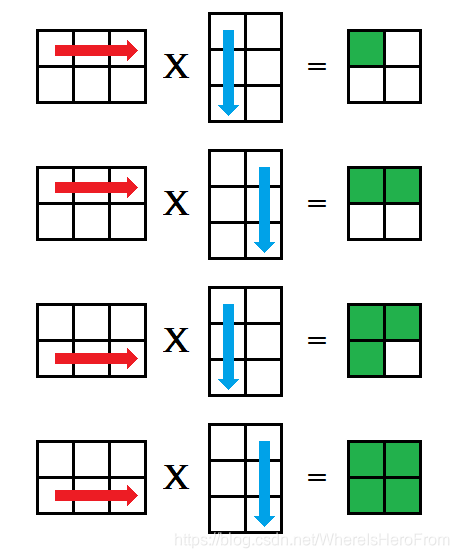
class Matrix { ...public: void Multiply_ijk(const Matrix& other, Matrix& ret) { // assert(m == other.n); ret.Reset(n, other.m); int i, j, k; for (i = 0; i < n; i++) { for (j = 0; j < other.m; j++) { for (k = 0; k < m; k++) { ret.pkData[i][j] += pkData[i][k] * other.pkData[k][j]; } } } }}; - 这种方法被称为 i j k ijk ijk 式,对矩阵乘法 A × B = C A \times B = C A×B=C,枚举 A A A 的每一行,再枚举 B B B 的每一列,分别对应相乘后放入矩阵 C C C 的对应位置中,如下图所示;
2、 i k j ikj ikj 式
- 对上述算法进行一些改进,交换两个内层循环的位置,得到如下算法:
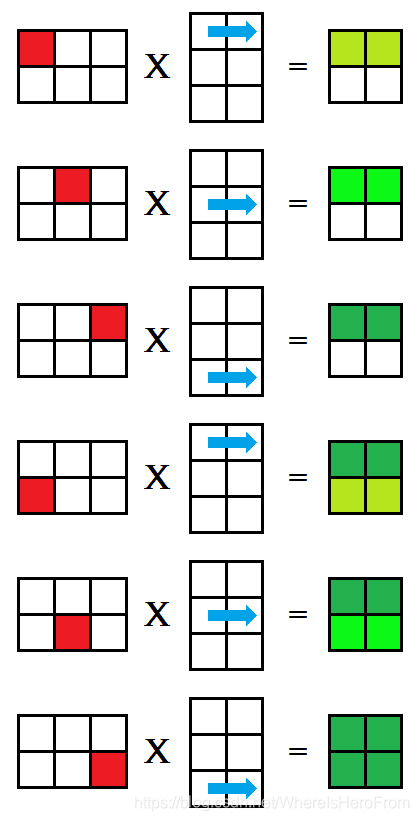
class Matrix { ...public: void Multiply_ikj(const Matrix& other, Matrix& ret) { // assert(m == other.n); ret.Reset(n, other.m); int i, j, k; for (i = 0; i < n; i++) { for (k = 0; k < m; k++) { LL v = pkData[i][k]; for (j = 0; j < other.m; j++) { ret.pkData[i][j] += v * other.pkData[k][j]; } } } }}; - 这种方法被称为 i k j ikj ikj 式,对矩阵乘法 A × B = C A \times B = C A×B=C,行优先枚举 A A A 的每一个格子,再枚举 B B B 的每一行,分别对应相乘后放入矩阵 C C C 的对应位置中,每次相乘得到的 C C C 都是部分积,如下图所示,用绿色的深浅来表示这个值是否已经完整求得;
3、 k i j kij kij 式
- 对上述算法再进行一些改进,交换两个外层循环的位置,得到如下算法:
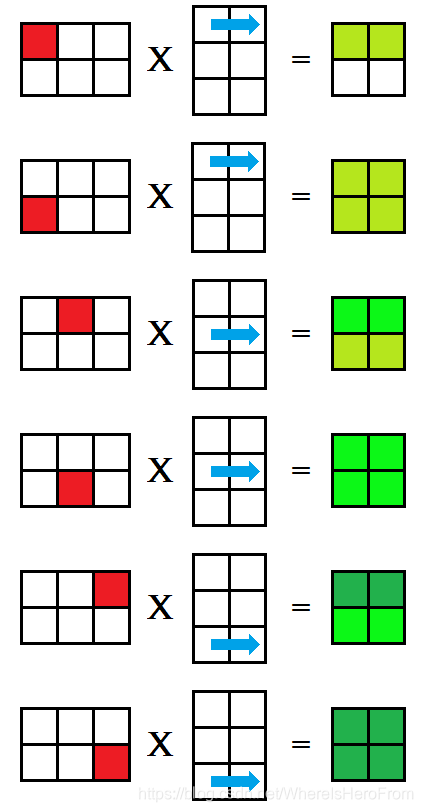
class Matrix { ...public: void Multiply_kij(const Matrix& other, Matrix& ret) { // assert(m == other.n); ret.Reset(n, other.m); int i, j, k; for (k = 0; k < m; k++) { for (i = 0; i < n; i++) { LL v = pkData[i][k]; for (j = 0; j < other.m; j++) { ret.pkData[i][j] += v * other.pkData[k][j]; } } } }}; - 这种方法被称为 k i j kij kij 式,对矩阵乘法 A × B = C A \times B = C A×B=C,列优先枚举 A A A 的每一个格子,再枚举 B B B 的每一行,分别对应相乘后放入矩阵 C C C 的对应位置中,每次相乘得到的 C C C 都是部分积,如下图所示,用绿色的深浅来表示这个值是否已经完整求得;
四、时间测试
| 矩阵阶数 | i j k ijk ijk | i k j ikj ikj | k i j kij kij |
|---|---|---|---|
| 200 | 47 ms | 31 ms | 16 ms |
| 500 | 781 ms | 438 ms | 453 ms |
| 1000 | 8657 ms | 3687 ms | 3688 ms |
| 2000 | 69547 ms | 28000 ms | 29672 ms |
- 由于矩阵乘法本身的时间复杂度是 O(N3) 的,所以数据量越大,越能看出实际效果;
五、原理分析
- 原因是因为 CPU 访问内存的速度比 CPU 计算速度慢得多,为了解决速度不匹配的问题,在 CPU 与 内存 之间加了高速缓存cache。高速缓存 cache 的存在大大提高了 CPU 访问数据的速度。但是当内存访问不连续的时候,就会导致 cache 命中率降低,所以为了加速,就要尽可能使内存访问连续,即不要跳来跳去。
- 矩阵
六、最后结论
- 运行速度: i k j ≈ k i j > i j k ikj \approx kij > ijk ikj≈kij>ijk
- 模板地址:
转载地址:http://lijdz.baihongyu.com/
你可能感兴趣的文章
Netty速成:基础+入门+中级+高级+源码架构+行业应用
查看>>
Netty遇到TCP发送缓冲区满了 写半包操作该如何处理
查看>>
netty(1):NIO 基础之三大组件和ByteBuffer
查看>>
Netty:ChannelPipeline和ChannelHandler为什么会鬼混在一起?
查看>>
Netty:原理架构解析
查看>>
Network Dissection:Quantifying Interpretability of Deep Visual Representations(深层视觉表征的量化解释)
查看>>
Network Sniffer and Connection Analyzer
查看>>
Network 灰鸽宝典【目录】
查看>>
Networkx写入Shape文件
查看>>
NetworkX系列教程(11)-graph和其他数据格式转换
查看>>
Networkx读取军械调查-ITN综合传输网络?/读取GML文件
查看>>
NetworkX:是否为每个节点添加超链接?
查看>>
network小学习
查看>>
Netwox网络工具使用详解
查看>>
Net与Flex入门
查看>>
Net任意String格式转换为DateTime类型
查看>>
net包之IPConn
查看>>
net发布的dll方法和类显示注释信息(字段说明信息)[图解]
查看>>
Net处理html页面元素工具类(HtmlAgilityPack.dll)的使用
查看>>
Net操作Excel(终极方法NPOI)
查看>>